| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- PHP 웹페이지 만들기
- c++
- HTML
- 백준
- 웹페이지 만들기
- 숙명여자대학교 정보보안 동아리
- lob
- hackctf
- 숙명여자대학교 정보보안동아리
- 파이썬
- siss
- 기계학습
- CSS
- hackerrank
- 드림핵
- 생활코딩
- The Loard of BOF
- WarGame
- Python
- BOJ Python
- Javascript
- BOJ
- c
- C언어
- 자료구조 복습
- SWEA
- 머신러닝
- Sookmyung Information Security Study
- 풀이
- XSS Game
- Today
- Total
혜랑's STORY
[바킹독 실전 알고리즘] 0x01 - 기초 코드 작성 요령1 본문
[실전 알고리즘] 0x01강 - 기초 코드 작성 요령 I
안녕하세요, 바킹독입니다. 이번 단원에서는 기초 코드 작성 요령을 익혀보려고 합니다. 목차를 보셨으면 알겠지만 기초 코드 작성 요령이 두 강으로 나눠져있는데 앞으로 코드를 잘 짜기 위해
blog.encrypted.gg
0x00 시간복잡도, 공간복잡도
시간복잡도
컴퓨터는 1초에 대략 3-5억 개 정도의 연산을 처리할 수 있다. 단, 연산이 AND, OR, 비교, 덧셈과 같은 단순한 연산인지 나눗셈, 곱셈, 대입, 합수 호출과 같은 복잡한 연산인지에 따라 횟수에 차이가 날 수 있다.
문제) 10이하의 두 자연수가 한 줄에 공백을 사이에 두고 주어진다. 두 자연수를 합한 결과를 출력하라. (단, 시간 제한은 1초, 메모리 제한은 256MB이다.)
입력) 3 6
출력) 9
위 문제에 대한 정답 코드는 아래와 같다.
#include <iostream>
using namespace std;
int main(){
int a, b;
cin >> a >> b;
cout << a + b;
}
이 코드는 06번째 줄에서 두 변수를 입력받을 때, 07번때 줄에서 두 수를 더하고 출력할 때 연산이 발생한다. 따라서 제한 시간인 1초 이내로 모든 명령어를 수행한 후 종료된다. 이처럼 간단한 프로그램의 경우 연산의 횟수를 셀 수 있지만, 아래 코드를 본다면 몇 번의 연산이 수행되는지 잘 감이 오지 않을 것이다.
int func1(int arr[], int n){
int cnt = 0;
for(int i = 0; i < n; i++)
if(arr[i] % 5 == 0) cnt++;
return cnt;
}
해당 함수는 arr[0]부터 arr[n-1]까지 for문을 실행하며 5로 나눈 나머지가 0이면(즉, arr[i]가 5의 배수라면) cnt 변수의 값을 1 증가시킨다. 따라서 n은 arr 배열의 크기이고, arr[0]부터 arr[n-1]까지의 5으 배수의 갯수를 반환하는 함수이다. 이 함수가 몇 번의 연산을 수행하는지 알아보자.
일단 02번째 줄에서 cnt 변수를 선언하고 0을 넣는 과정에서 1번, 03번째 줄에서 i에 초기 값으로 0을 대입할 때 1번, 그 다음에는 n번을 걸쳐 i가 n보다 작은지 확인하고 작을 경우 1을 증가시키는 연산이 2번 진행된다. 04번째 줄에서 5로 나눈 나머지를 계산하고 그게 0과 일치하는지 확인할 때 연산 2번, 만약 5의 배수라면 cnt를 1 증가시키는 연산 1번, 마지막으로 cnt를 반환할 때 연산 1번이 필요하게 된다.
따라서 1 + 1 + n x (2 + 2 + 1) + 1 = 5n + 3이 되고, 이 함수는 5n + 3번의 연산이 필요하다는 것을 알 수 있다. 이때 n이 100만 정도라면 대충 500만 번의 연산이 필요하니 1초 안에 충분히 실행이 가능하지만, n이 10억이라면 50억 번의 연산을 필요로 하니 1초안에 실행이 불가능하다.
그런데 매번 이렇게 코드를 실행 단위로 뜯어보는 것은 너무 많은 시간 낭비가 발생하게 된다. 그렇게 때문에 n이 무한히 커질때를 생각하여 상수는 제외하고 대강 n에 비례한다고 이야기 한다. 이 사실을 빠르게 생각하는 방법으로는 for문에서 n번에 걸쳐 5로 나눈 나머지를 확인하고 0과 일치하면 cnt를 증가시키는 행위를 하니 n에 비례한다는 유추를 할 수 있게 되는 것이다.
문제) 대회장에 N명의 사람들이 일렬로 서있다. 거기서 당신은 이름이 '가나다'인 사람을 찾기 위해 사람들에게 이름을 물어볼 것이다. 이름을 물어보고 대답을 듣는데까지 1초가 걸린다면 얼마만큼의 시간이 필요할까?
만약 1번째 사람에게 이름을 물어보았을 때 '가나다'씨가 맞다면 1초가 걸릴 것이고, 최악의 경우인 N번째에 '가나다'씨를 찾게 되면 N초가 걸리게 될 것이다. 평균적으로는 절반쯤 물어보고 '가다나'씨를 찾는 경우인 N/2초이다.
이렇게 걸리는 시간은 N에 비례하게 된다. 사람이 100명이면 대충 50초정도 걸릴 것이고, 사람이 10배 늘어나면 걸리는 시간도 10배 늘어나서 500초 정도 걸리게 될 것이다.
문제) 대회장에 N명의 사람들이 일렬로 서있다. 거기서 당신은 이름이 '가나다'인 사람을 찾기 위해 사람들에게 이름을 물어볼 것이다. 이때 사람들은 이름 순으로 서있다. 이름을 물어보고 대답을 듣는데까지 1초가 걸린다면 얼마만큼의 시간이 필요할까?
앞의 문제와 거의 비슷하지만 이름 순으로 서있다는 조건 1개가 추가되었다. 이 문제에서 '가나다'씨를 찾는 것은 얼마나 걸리게 될까? N명의 사람들 중 가운데 있는 사람의 이름을 물었을 때 '가나다'보다 뒤에 있어야 하는 이름이면 '가나다'는 앞쪽 그룹에 있을 것이다. 마찬가지로 '가나다'보다 앞에 있어야 하는 이름이면 '가나다'는 뒤쪽 그룹에 있을 것이다.
최선의 경우는 맨 처음 물어본 사람이 바로 '가나다'인 경우이고 이때 시간은 1초가 소요된다. 최악의 경우에는 마지막 1명이 남을 때 까지 후보군을 절반씩 줄여가는 상황이고, 이는 lg N초가 소요될 것이다. (로그의 및은 항상 2이다.) 평균적으로는 (1 - 1/N) lg N 이지만, N이 커질수록 0에 가까운 값이 되므로 대략적으로 lg N초가 걸린다고 말 할 수 있다.
위 두 문제를 통해 시간복잡도는 입력의 크기와 문제를 해결하는 데 걸리는 시간의 상관관계라는 것을 알 수 있다.

시간복잡도와 함께 빅오표기법(Big-O notation)이 등장하는데 이는 알고리즘이 해당 차수이거나 그보다 낮은 차수의 시간복잡도를 가진다는 의미이다. 예를 들어 디스크에 있는 파일을 다른 지역에 살고 있는 친구에게 보낸다고 가정해보자. 파일의 크기가 작다면, 즉 n이 작다면 O(n)의 시간이 걸리는 온라인 전송이 빠를 것이다. 그러나 파일이 아주 크다면 비행기를 통해 물리적으로 배달하는 것이 더 빠를 수 있다. 파일(n)이 아무리 커도 비행기를 통한 파일 전송은 O(1)로 항상 일정한 시간이 소요되기 때문이다. 이것이 바로 점근적 실행 시간이며, 빅오는 점근적 실행 시간을 표기하는 방법 중 하나이다.
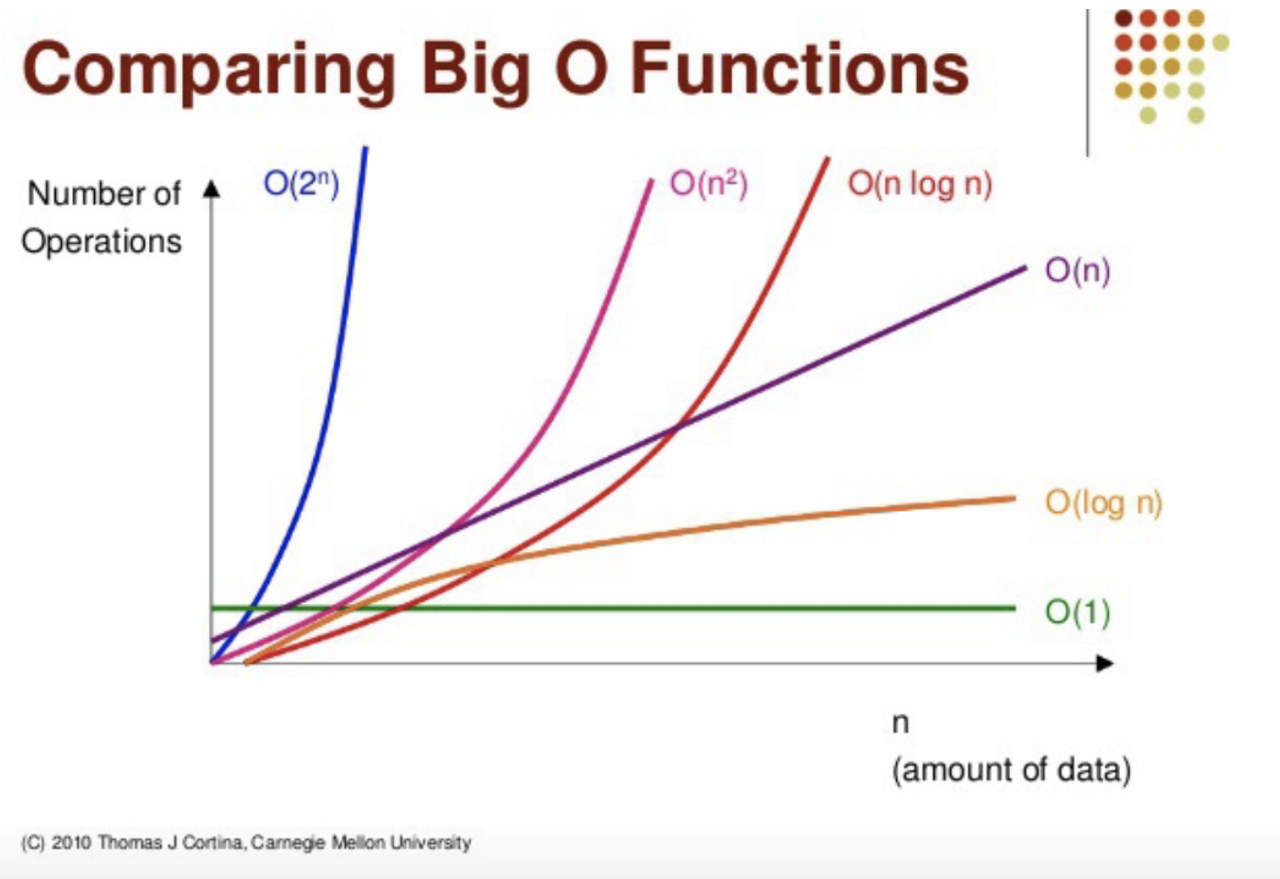
그래프를 보면 알 수 있듯이 상수 시간인 O(1)이 가장 좋고, 그 다음으로 O(lg N)이 좋다. 이후로 O(N), O(N lg N), O(N^2)이 있다. O(lg N)은 로그 시간, O(N)은 선형 시간이라 부르고, O(lg N)부터 O(N^2)까지와 같이 lg N 혹은 N의 거듭제곱끼리의 곱으로 시간복잡도가 나타내지면 이를 다항 시간이라고 한다.
O(N^2)은 지수 시간으로 N이 25 이하 정도로 굉장히 작은 게 아니라면 시간 제한을 통과하기 힘들 것이다. O(n!)은 지수 시간보다도 훨씬 더 가파르게 올라가므로 N이 11 정도로 작은 것이 아니라면 시간 제한을 통과하기 힘들다.
| N의 크기 | 허용 시간복잡도 |
| N <= 11 | O(N!) |
| N <= 25 | O(2^N) |
| N <= 100 | O(N^4) |
| N <= 500 | O(N^3) |
| N <= 3,000 | O(N^2 lg N) |
| N <= 5,000 | O(N^2) |
| N <= 1,000,000 | O(N lg N) |
| N <= 10,000,000 | O(N) |
| 그 이상 | O(1), O(lg N) |
문제에서 주어지는 시간 제한은 대부분 1초에서 5초 사이 정도로 입력의 범위를 보고 문제에서 요구하는 시간복잡도가 어느 정도인지를 알 수 있다. 예를 들어 주어진 배열을 크기 순으로 정렬하는 문제를 생각하면 O(N lg N)으로 해결할 수 있고 O(N^2)의 방법도 있다. N이 1,000 이하라면 둘 중 어느 것을 사용하더라도 빠르게 문제를 해결할 수 있겠지만, N이 100만이라면 O(N lg N)은 1초 내로 정렬이 완료되지만 O(N^2)은 약 1시간 정도 시간을 필요로 한다.
이런식으로 N의 크기에 따른 허용 시간복잡도를 표로 나타낸 것이다. 절대적 기준은 아니지만 대략적으로 위와 같다고 생각하면 된다.
앞으로 문제를 풀 때는 풀이가 제한 시간 내로 통과할 수 있는지 즉, 알고리즘 내의 시간복잡도가 올바른지를 꼭 생각해 보아야 한다.
문제1) N 이하의 자연수 중 3의 배수이거나 5의 배수인 수를 모두 합한 값을 반환하는 함수 func1(int N)을 작성하라. N은 5만 이하의 자연수이다.
예시) func1(16) = 60 / func1(34567) = 278812814 / func1(27639) = 178254968
위 문제에 대해 내가 작성한 코드는 다음과 같다.
int func1(int N)
{
int sum = 0;
for(int i=1; i<=N; i++){
if(i % 3 == 0) sum += i;
else if(i % 5 == 0) sum += i;
}
return sum;
}
코드를 보면 for문에서 i는 1부터 N까지 실행되며 3 또는 5로 나누어지는지 확인하는 것을 알 수 있다. 즉, 시간복잡도는 O(N)이다.
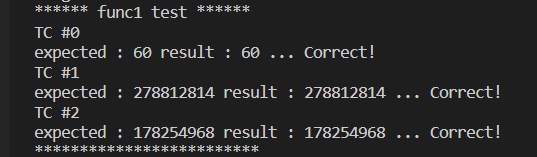
작성한 코드를 실행했을 때 결과이다.
문제2) 주어진 길이 N의 int 배열 arr에서 합이 100인 서로 다른 위치의 두 원소가 존재한다면 1을 존재하지 않으면 0을 반환하는 함수 func2(int arr[], int N)을 작성하라. arr의 각 수는 0 이상 100 이하이고 N은 1,000 이하이다.
예시) func({1, 52, 48}, 3) = 1 / func2({50, 42}, 2} = 0, func2({4, 13, 63, 87}, 4) = 1
위 문제에 대해 내가 작성한 코드는 다음과 같다.
int func2(int arr[], int N)
{
for(int i=0; i<N-1; i++){
for(int j=i+1; j<N; j++){
if(arr[i] + arr[j] == 100) return 1;
}
}
return 0;
}
코드를 보면 이중 for문을 사용하는 것을 알 수 있다. 즉, 시간 복잡도는 O(N^2)가 된다.
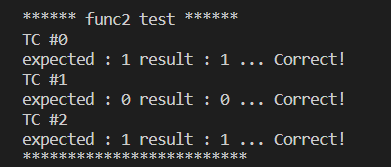
작성한 코드가 잘 실행됨을 알 수 있다. 위 풀이 말고 O(N) 풀이가 존재한다고 하니, 공부를 진행하고 O(N) 풀이에 도전해보자!
문제3) N이 제곱수이면 1을 반환하고 제곱수가 아니면 0을 반환하는 함수 func3(int N)을 작성하라. N은 10억 이하의 자연수이다.
예시) func3(9) = 1 / func3(693953651) = 0 / fun3(756480036) = 1
아래는 내가 작성한 코드이다.
int func3(int N)
{
for(int i = 2; i*i <= N; i++){
if(i*i == N) return 1;
}
return 0;
}for문을 사용해 i가 2부터 N까지 올라가면서 i의 제곱이 N과 일치하는지 확인하다가 일치하는 순간이 있으면 N이 제곱수이니 1을 반환했다. 이때의 시간 복잡도는 O(√N)가 된다.
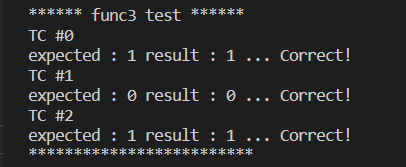
이 문제 또한 O(lg N)의 풀이가 있다고 하니 강의를 들으며 다시 도전해보자.
문제4) N이하의 수 중 가장 큰 2의 거듭제곱수를 반환하는 함수 func4(int N)을 작성하라. N은 10억 이하의 자연수이다.
예시) func4(5) = 4 / func4(97615282) = 67108864 / func4(1024) = 1024
풀어봤다.
int func4(int N)
{
int num;
for(num = 1; num*2 <= N; num *= 2);
return num;
}위 방식에서 시간복잡도는 얼마일까? N이 2^k 이상 2^(k+1) 미만이라고 할 때 for문에서 num은 최대 k번 2배로 커진다. 이때 시간복잡도는 O(k)가 되고 k는 lg N가 되니까 결과적으로 O(lg N)이 된다.
공간복잡도
공간복잡도는 입력의 크기와 문제를 해결하는데 필요한 공간의 상관관계이다. 예를 들어 크기가 N인 2차원 배열이 필요하다면 O(N^2)이고, 따로 배열이 필요하지 않다면 O(1)이 된다. 메모리 제한이 512MB일 때, int 변수를 대략 1.2억개 정도 선언할 수 있다. (int 1개가 4byte)
0x01 정수 자료형
'char 자료형은 1byte = 8bit이다.'라는 말은 아래와 같이 8개의 0 혹은 1이 들어가는 값으로 표현된다는 의미이다. (= 8bit레 2진수 표기로 값이 들어간다.)
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
오른쪽부터 2^0, 2^1, 2^2 ... 2^6을 나타낸다. unsigned char에서는 제일 왼쪽이 2^7을 의미하지만, char에서는 독특하게 -2^7이다. (2's complement로 인해) 즉, 1000 0011을 unsigned char로 읽으면 131이고 char로 읽으면 -125가 된다.
unsigned char로 표현할 수 있는 수의 최솟값은 0000 0000인 0이고, 최댓값은 1111 1111인 255가 된다. char에 대해서도 똑같이 표현할 수 있는 최솟값과 최댓값을 구해보면 최솟값은 1000 0000일 때 -128일 것이고, 최댓값은 0111 1111인 127이 될 것이다.
정수 자료형에는 char 말고도 short, int, long long 자료형이 있다. 각각 2byte, 4byte, 8byte이다. char의 크기를 계산한 것처럼 각각 표현할 수 있는 최댓값을 확인하면 32767, 대략 2.1x10^9(21억), 9.2x10^18까지 표현할 수 있다. short는 자주 사용되지 않고 정수를 표현할 때 주로 int나 long long을 사용하는데 int가 long long보다 연산 속도와 메모리 모두 우수하지만 표현할 수 있는 범위를 넘어서는 수를 저장해야 할 때는 long long 자료형을 사용해야 한다.
Integer Overflow
int main(void){
int a = 2000000000 * 2;
cout << a;
}
// result: -294967296int가 대략 21억까지 표시할 수 있으니 20억에 2를 곱한 40억을 저장할 수 없다는 것은 당연하다. 그런데 '-294967296'은 어디서 나온 값일까? 이런 현상이 바로 Integer Overflow이다. 관찰을 위해 아래 두 char 자료형의 수를 더해보자.
- 2^3 + 2^0 = 9
| 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
- 2^4 + 2^2 + 2^0 = 21
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
- 2^4 + 2^3 + 2^2 + 2^1 = 30
| 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 |
이진수의 덧셈으로 보았을 때도 1001과 10101을 더하면 11110이 된다는 것을 알 수 있다. 음수가 섞인 덧셈도 크게 고민할 것 없이 이진수의 덧셈으로 해결할 수 있다.
- -2^7 + 2^3 + 2^0 = -119
| 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 |
- 2^2 + 2^0 = 5
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 |
- -2^7 + 2^3 + 2^2 + 2^1 = -114
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 0 |
그런데 char의 최댓값인 127에 1을 더하면 어떻게 될까?
- 127
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
- 1
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
- -128
| 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
1111 1111에 0000 0001을 더하니 1000 0000이 되었다. 따라서 char의 제일 왼쪽칸은 -2^7이므로 -128의 값을 가지게 되는 것이다. 컴퓨터는 명령받은 대로 이진수를 계산했을 뿐인데 Integer Overflow의 결고로 옳지 않은 값이 나오게 된 것이다.
// 128번에 걸쳐 hi를 출력하는 함수
void func1(){
for(char s = 0; s < 128; s++)
cout << "hi" << endl;
}// 50!을 61로 나눈 나머지를 반환하는 함수
int func2(){
int r = 1;
for(int i=1; i<=50; i++)
r = r * i % 61;
}// 10의 10 거듭제곱을 1000000007로 나눈 나머지를 반환하는 함수
int func3(){
int a = 1;
int mod = 1000000007;
for(int i=0; i<10; i++)
a = 10 * a % mod;
return a;
}
위 3가지 함수 중 Integer Overflow로 인해 의도한대로 동장하지 않는 함수는 func1과 func3이다. func1의 경우 s가 127이 된 후에 1이 더해지기 때문에 -128이 되어 의도한대로 동작하지 않고 무한루프에 빠지게 된다. 이를 해결하기 위해서는 s의 자료형을 char에서 int로 바꿔줘야 한다. func3의 경우 a가 10^9일 때 여기서 10이 곱해지는 순간 int의 최대 범위를 넘어 Integer Overflow가 발생한다. 이를 막기 위해서는 a의 자료형을 long long으로 바꾸거나 6번째 줄에서 곱해주는 10을 10ll으로 하여 (long long)10으로 강제 형변환을 시켜 해결할 수도 있다. 만약 문제에서 unsigned long long 범위를 넘어서는 수를 저장할 것을 요구하는 경우 string을 활용하여 저장해야 한다.
0x02 실수 자료형
실수 자료형으로는 float과 double이 있다. float은 4byte이고 double은 8byte이다. 정수형과 비슷하게 생각해보면 0 또는 1이 들어가는 32칸/64칸으로 실수를 나타내는 것이다.
정수를 2진수로 바꿀 때 2^0, 2^1, 2^2 ,,, 2^n의 합으로 나타낸 것처럼 실수를 2진수로 바꿀 땐 2^(-1), 2^(-2), 2^(-3) ,,, 2^(-n)의 합으로 나타내면 된다. 즉, 2의 음수 거듭제곱을 이용해 임의의 실수를 2진수로 나타낼 수 있는 것이다.
예) 3.75 = 2^1 + 2^0 + 2^(-1) + 2^(-2) = 11.11
실수를 나타낼 때 칸은 sign, exponent, fraction field로 나누어진다. sign field는 해당 수가 음수인지 양수인지 저장하는 필드이고, exponent field는 과학적 표기법에서의 지수를 저장하는 필드이다. 마지막으로 fraction field는 유효숫자 부분을 저장하는 필드이다. 각 필드의 크기는 float의 경우 1, 8 23 bit이고 double은 1, 11, 52 bit이다.
예) -6.75 = - 1.1011 x 2^2
==> -6.75의 부호가 음수여서 sign은 1이된다. 2의 2승이 곱해지기 때문에 지수는 2이고 float에서는 여기에 127을 더한 129를 exponent field에 기록한다. (127을 더하는 이유는 음수 지수승도 exponent field에 넣기 위해서이다. double의 경우 exponent field가 11칸이기 때문에 1023을 더한다.) 마지막으로 fraction field에는 맨 앞의 1은 뺀 1011을 적게된다. 맨 왼쪽부터 2^(-1), 2^(-2)자리인 셈이다.
| sign(1) | exponent(1000 0001) | fraction(1011 0000 ,,, 0000) |
실수의 성질
- 1. 실수의 저장/연산 과정에서 반드시 오차가 발생할 수 밖에 없다.
- double에 long long 범위의 정수를 함부로 담으면 안된다. (오차가 발생함. 다만, int는 최대 21억이기 떄문에 double에 담아도 오차가 생기지 않는다.)
- 실수를 비교할 때는 등호를 사용하지 않는다. (오차가 발생하기 때문에 두 실수가 같은지 알고 싶다면 둘 차이가 아주 작은 값, 대략 10^(-12) 이하면 동일하다고 처리하는 것이 안전하다.)
